Homework6
Sam Troast
2025-02-19
library(tidyverse)## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.5.1
## ✔ ggplot2 3.5.1 ✔ tibble 3.2.1
## ✔ lubridate 1.9.4 ✔ tidyr 1.3.1
## ✔ purrr 1.0.2
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorslibrary(ggplot2)Question 1 I will be simulating a lab experiment where eastern newts are held at different temperatures (Hot - 22C, Moderate - 18C, & Cool - 10C) to measure Bd load over time. I expect newts at higher temperatures will have lower Bd amounts at the end of the study.
Question 2
Hot(22C): sample size = 100, mean = 250, sd = 10
Moderate(18C): sample size = 100, mean = 300, sd = 10
Cool(10C): sample size = 100, mean = 100, sd = 12
Question 3
nGroup <- 3 # number of groups
nName <- c("Hot","Moderate","Cool") # names of groups
nSize <- c(100,100,100) # number of observations in each group
nMean <- c(250,300,100) # mean of each group
nSD <- c(10,10,12) # standard deviation of each group
ID <- 1:(sum(nSize)) # create id vector for each row
Bd_load <- c(rnorm(n=nSize[1],mean=nMean[1],sd=nSD[1]),
rnorm(n=nSize[2],mean=nMean[2],sd=nSD[2]),
rnorm(n=nSize[3],mean=nMean[3],sd=nSD[3]))
Temperature <- rep(nName,nSize)
newtdata <- data.frame(ID,Temperature,Bd_load)
newtdata## ID Temperature Bd_load
## 1 1 Hot 242.58739
## 2 2 Hot 240.66887
## 3 3 Hot 268.17618
## 4 4 Hot 261.34112
## 5 5 Hot 252.88497
## 6 6 Hot 240.65523
## 7 7 Hot 254.83238
## 8 8 Hot 250.38474
## 9 9 Hot 249.00754
## 10 10 Hot 248.82493
## 11 11 Hot 260.49755
## 12 12 Hot 253.90582
## 13 13 Hot 233.61782
## 14 14 Hot 237.76052
## 15 15 Hot 243.34021
## 16 16 Hot 260.67087
## 17 17 Hot 261.89251
## 18 18 Hot 261.99967
## 19 19 Hot 243.83823
## 20 20 Hot 245.84451
## 21 21 Hot 250.14348
## 22 22 Hot 242.25228
## 23 23 Hot 269.03012
## 24 24 Hot 251.03336
## 25 25 Hot 236.07061
## 26 26 Hot 251.48845
## 27 27 Hot 253.41984
## 28 28 Hot 266.55362
## 29 29 Hot 245.78616
## 30 30 Hot 265.76294
## 31 31 Hot 247.31829
## 32 32 Hot 255.36224
## 33 33 Hot 236.63228
## 34 34 Hot 254.51130
## 35 35 Hot 269.03845
## 36 36 Hot 249.41809
## 37 37 Hot 241.13620
## 38 38 Hot 245.11857
## 39 39 Hot 242.68409
## 40 40 Hot 274.75172
## 41 41 Hot 255.30971
## 42 42 Hot 270.32081
## 43 43 Hot 251.78016
## 44 44 Hot 244.86095
## 45 45 Hot 254.28503
## 46 46 Hot 261.42395
## 47 47 Hot 250.91201
## 48 48 Hot 252.30912
## 49 49 Hot 248.05477
## 50 50 Hot 256.90945
## 51 51 Hot 254.53452
## 52 52 Hot 249.36484
## 53 53 Hot 242.73295
## 54 54 Hot 264.57631
## 55 55 Hot 235.74992
## 56 56 Hot 265.32040
## 57 57 Hot 267.14537
## 58 58 Hot 233.45645
## 59 59 Hot 248.84180
## 60 60 Hot 243.89788
## 61 61 Hot 255.79397
## 62 62 Hot 267.39177
## 63 63 Hot 264.15964
## 64 64 Hot 259.22514
## 65 65 Hot 242.43430
## 66 66 Hot 240.43621
## 67 67 Hot 247.73132
## 68 68 Hot 243.26503
## 69 69 Hot 252.16397
## 70 70 Hot 249.07557
## 71 71 Hot 242.73015
## 72 72 Hot 242.63444
## 73 73 Hot 245.54479
## 74 74 Hot 247.07192
## 75 75 Hot 255.33717
## 76 76 Hot 231.90352
## 77 77 Hot 257.18615
## 78 78 Hot 260.77873
## 79 79 Hot 258.30886
## 80 80 Hot 241.86930
## 81 81 Hot 247.90904
## 82 82 Hot 230.28840
## 83 83 Hot 230.59729
## 84 84 Hot 232.19938
## 85 85 Hot 252.32012
## 86 86 Hot 250.76748
## 87 87 Hot 268.92480
## 88 88 Hot 256.38607
## 89 89 Hot 257.36225
## 90 90 Hot 244.63894
## 91 91 Hot 229.92816
## 92 92 Hot 236.48286
## 93 93 Hot 256.94996
## 94 94 Hot 246.85555
## 95 95 Hot 247.78063
## 96 96 Hot 241.28827
## 97 97 Hot 242.74403
## 98 98 Hot 267.99392
## 99 99 Hot 257.82418
## 100 100 Hot 247.44623
## 101 101 Moderate 303.20014
## 102 102 Moderate 291.01047
## 103 103 Moderate 291.65189
## 104 104 Moderate 311.57803
## 105 105 Moderate 292.39245
## 106 106 Moderate 300.25247
## 107 107 Moderate 293.17468
## 108 108 Moderate 292.09074
## 109 109 Moderate 304.41280
## 110 110 Moderate 309.75425
## 111 111 Moderate 301.62941
## 112 112 Moderate 297.18123
## 113 113 Moderate 294.86238
## 114 114 Moderate 310.02812
## 115 115 Moderate 294.40540
## 116 116 Moderate 295.68779
## 117 117 Moderate 304.74504
## 118 118 Moderate 292.08410
## 119 119 Moderate 296.41028
## 120 120 Moderate 287.46371
## 121 121 Moderate 304.77123
## 122 122 Moderate 321.15061
## 123 123 Moderate 301.76714
## 124 124 Moderate 295.30275
## 125 125 Moderate 304.67881
## 126 126 Moderate 284.41204
## 127 127 Moderate 299.98307
## 128 128 Moderate 281.29805
## 129 129 Moderate 311.87001
## 130 130 Moderate 279.69541
## 131 131 Moderate 300.76039
## 132 132 Moderate 280.55105
## 133 133 Moderate 292.57285
## 134 134 Moderate 299.70018
## 135 135 Moderate 298.86084
## 136 136 Moderate 290.80244
## 137 137 Moderate 303.75845
## 138 138 Moderate 290.50727
## 139 139 Moderate 298.75239
## 140 140 Moderate 302.17598
## 141 141 Moderate 292.26457
## 142 142 Moderate 302.26770
## 143 143 Moderate 296.18975
## 144 144 Moderate 296.13528
## 145 145 Moderate 308.00657
## 146 146 Moderate 295.98716
## 147 147 Moderate 317.08453
## 148 148 Moderate 287.69094
## 149 149 Moderate 295.72556
## 150 150 Moderate 299.39427
## 151 151 Moderate 319.97372
## 152 152 Moderate 289.00223
## 153 153 Moderate 298.90926
## 154 154 Moderate 288.17481
## 155 155 Moderate 304.33506
## 156 156 Moderate 303.91514
## 157 157 Moderate 301.40151
## 158 158 Moderate 288.81177
## 159 159 Moderate 309.30665
## 160 160 Moderate 282.27009
## 161 161 Moderate 305.26606
## 162 162 Moderate 297.02861
## 163 163 Moderate 324.34395
## 164 164 Moderate 302.71668
## 165 165 Moderate 289.47238
## 166 166 Moderate 306.54892
## 167 167 Moderate 313.68053
## 168 168 Moderate 304.17179
## 169 169 Moderate 296.96505
## 170 170 Moderate 287.06750
## 171 171 Moderate 301.76520
## 172 172 Moderate 286.43810
## 173 173 Moderate 302.96398
## 174 174 Moderate 285.74479
## 175 175 Moderate 285.74917
## 176 176 Moderate 313.21421
## 177 177 Moderate 305.33980
## 178 178 Moderate 301.52331
## 179 179 Moderate 286.77076
## 180 180 Moderate 289.35915
## 181 181 Moderate 295.59354
## 182 182 Moderate 297.36358
## 183 183 Moderate 299.46071
## 184 184 Moderate 288.39590
## 185 185 Moderate 303.54408
## 186 186 Moderate 315.94896
## 187 187 Moderate 305.27501
## 188 188 Moderate 313.20514
## 189 189 Moderate 280.78445
## 190 190 Moderate 286.83910
## 191 191 Moderate 306.36002
## 192 192 Moderate 302.19550
## 193 193 Moderate 297.98891
## 194 194 Moderate 306.87596
## 195 195 Moderate 300.32485
## 196 196 Moderate 317.07936
## 197 197 Moderate 301.37788
## 198 198 Moderate 308.95559
## 199 199 Moderate 299.74694
## 200 200 Moderate 305.07179
## 201 201 Cool 127.58763
## 202 202 Cool 116.25819
## 203 203 Cool 100.00221
## 204 204 Cool 123.49113
## 205 205 Cool 96.25259
## 206 206 Cool 102.95519
## 207 207 Cool 100.84972
## 208 208 Cool 116.04065
## 209 209 Cool 94.28438
## 210 210 Cool 93.75056
## 211 211 Cool 112.03662
## 212 212 Cool 98.87514
## 213 213 Cool 93.78767
## 214 214 Cool 89.83881
## 215 215 Cool 90.78846
## 216 216 Cool 101.07700
## 217 217 Cool 111.75615
## 218 218 Cool 90.94989
## 219 219 Cool 100.63012
## 220 220 Cool 83.53886
## 221 221 Cool 107.47453
## 222 222 Cool 108.73119
## 223 223 Cool 92.13685
## 224 224 Cool 87.57865
## 225 225 Cool 96.96413
## 226 226 Cool 100.71422
## 227 227 Cool 102.37527
## 228 228 Cool 123.20222
## 229 229 Cool 91.30177
## 230 230 Cool 94.73061
## 231 231 Cool 98.32257
## 232 232 Cool 121.68412
## 233 233 Cool 101.41531
## 234 234 Cool 117.43687
## 235 235 Cool 121.32199
## 236 236 Cool 91.20772
## 237 237 Cool 104.23532
## 238 238 Cool 82.01781
## 239 239 Cool 92.59216
## 240 240 Cool 94.37928
## 241 241 Cool 111.06704
## 242 242 Cool 84.82383
## 243 243 Cool 108.56390
## 244 244 Cool 79.40199
## 245 245 Cool 88.79369
## 246 246 Cool 91.89720
## 247 247 Cool 100.27389
## 248 248 Cool 94.24112
## 249 249 Cool 111.51296
## 250 250 Cool 110.36950
## 251 251 Cool 93.69568
## 252 252 Cool 71.90545
## 253 253 Cool 117.01268
## 254 254 Cool 98.87076
## 255 255 Cool 102.12052
## 256 256 Cool 92.59518
## 257 257 Cool 111.55096
## 258 258 Cool 117.34823
## 259 259 Cool 106.68235
## 260 260 Cool 98.93019
## 261 261 Cool 117.88592
## 262 262 Cool 66.43419
## 263 263 Cool 100.14746
## 264 264 Cool 78.16112
## 265 265 Cool 103.49236
## 266 266 Cool 92.64669
## 267 267 Cool 95.63982
## 268 268 Cool 99.47692
## 269 269 Cool 117.50286
## 270 270 Cool 107.77020
## 271 271 Cool 100.16073
## 272 272 Cool 100.12740
## 273 273 Cool 108.58853
## 274 274 Cool 110.78672
## 275 275 Cool 111.46704
## 276 276 Cool 97.93661
## 277 277 Cool 102.70227
## 278 278 Cool 114.95210
## 279 279 Cool 112.60389
## 280 280 Cool 102.68002
## 281 281 Cool 120.81681
## 282 282 Cool 105.70166
## 283 283 Cool 90.19598
## 284 284 Cool 123.19431
## 285 285 Cool 74.83515
## 286 286 Cool 79.27908
## 287 287 Cool 92.62972
## 288 288 Cool 113.64110
## 289 289 Cool 114.87899
## 290 290 Cool 108.12761
## 291 291 Cool 113.15502
## 292 292 Cool 108.99827
## 293 293 Cool 111.52752
## 294 294 Cool 111.74059
## 295 295 Cool 105.63896
## 296 296 Cool 97.64590
## 297 297 Cool 117.67164
## 298 298 Cool 115.66225
## 299 299 Cool 103.80577
## 300 300 Cool 91.12011Question 4
newtdatamodel <- aov(Bd_load~Temperature, data=newtdata)
print(newtdatamodel)## Call:
## aov(formula = Bd_load ~ Temperature, data = newtdata)
##
## Terms:
## Temperature Residuals
## Sum of Squares 2106720.3 34732.2
## Deg. of Freedom 2 297
##
## Residual standard error: 10.81404
## Estimated effects may be unbalancedsummary(newtdatamodel)## Df Sum Sq Mean Sq F value Pr(>F)
## Temperature 2 2106720 1053360 9007 <2e-16 ***
## Residuals 297 34732 117
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1ggplot(data=newtdata,aes(x=Temperature,y=Bd_load,fill=Temperature)) + geom_boxplot() + scale_fill_manual(values= c("blue","red","green"))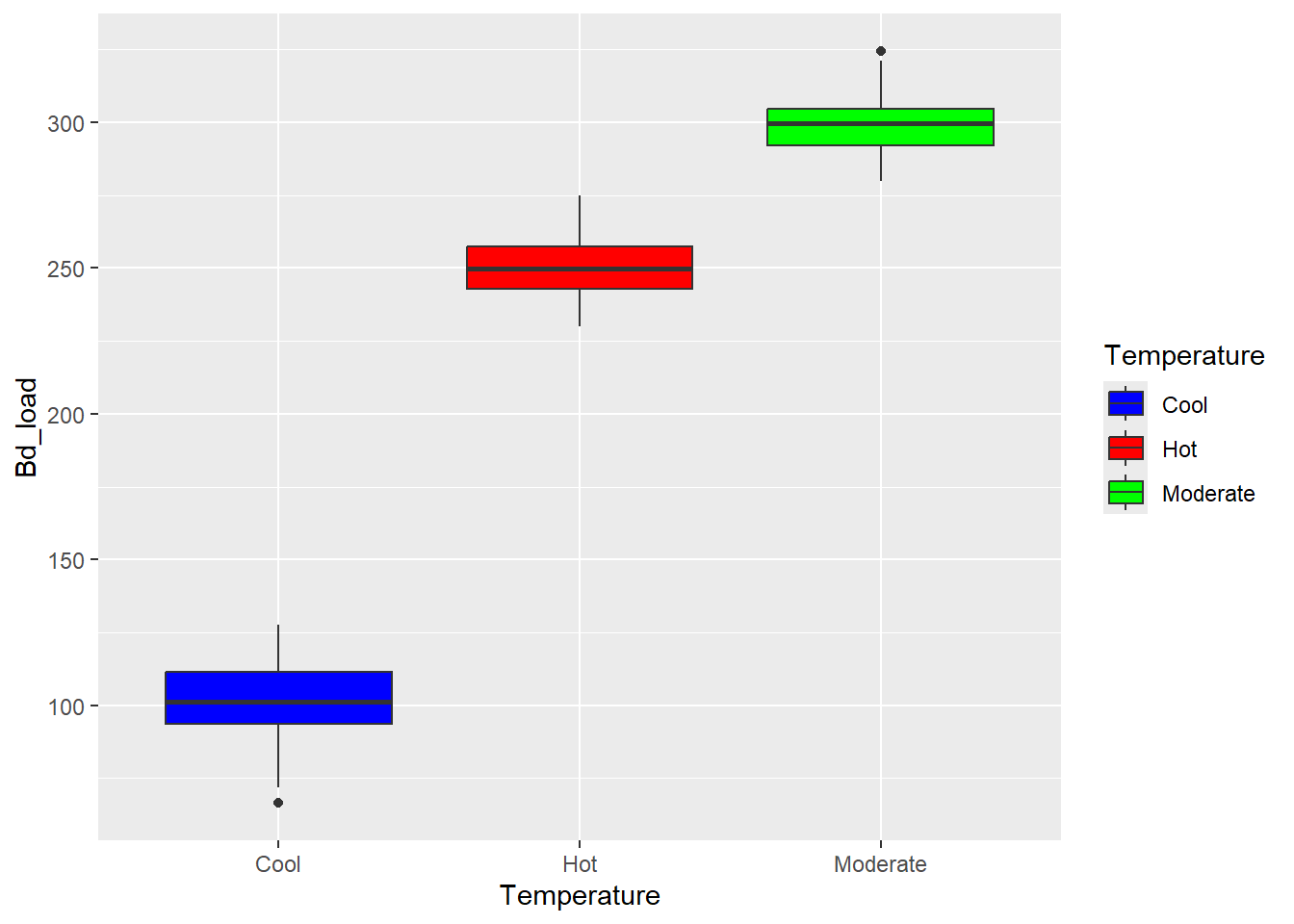
Question 5
First run: F = 1417748, p = <2e-16
Second run: F = 196729, p = <2e-16
Third run: F = 214829, p = <2e-16
After rerunning my analysis several times with different random numbers, we can see that we consistently get a very large F-value and a very small p-value, indicating that there is quite a significant difference regardless of the input data. We do see some variation within both values across the different runs, however we consistently come up with the same conclusion: there is a significant difference in Bd loads between temperature groups.
Question 6
results <- data.frame(sample_size = integer(),
effect_size = numeric(),
trait = character(),
p_value = numeric())
temps <- c("Hot", "Moderate", "Cool")
for (n in seq(10, nrow(newtdata), by = 5)) { # Increase sample size by 5 each iteration
# Randomly sample n observations
temp_data <- newtdata[sample(1:nrow(newtdata), n, replace = TRUE), ]
# Fit the model on the sampled data
mod <- aov(Bd_load ~ Temperature, data = temp_data)
# Extract coefficients and p-values for each level of the Temperature factor
for (temp in temps) {
# Check if the temperature level is a factor level
if (temp %in% levels(temp_data$Temperature)) {
# Extract the effect size (the coefficient) for the specific temperature level
effect_size <- coef(mod)[paste("Temperature", temp, sep = "")]
p_value <- summary(mod)[[1]]["Temperature", temp, 4] # p-value for the temp
# Store results
results <- rbind(results, data.frame(sample_size = n,
trait = temp,
effect_size = effect_size,
p_value = p_value))
}
}
}Question 7
nGroup <- 3 # number of groups
nName <- c("Hot","Moderate", "Cool") # names of groups
nSize <- c(2,2,2) # number of observations in each group
nMean <- c(250,500,100) # mean of each group
nSD <- c(1.25,1.1,1.2) # standard deviation of each group
ID <- 1:(sum(nSize)) # create id vector for each row
Hatch_time <- c(rnorm(n=nSize[1],mean=nMean[1],sd=nSD[1]),
rnorm(n=nSize[2],mean=nMean[2],sd=nSD[2]),
rnorm(n=nSize[3],mean=nMean[3],sd=nSD[3]))
Temperature <- rep(nName,nSize)
newtdata <- data.frame(ID,Temperature,Bd_load)
newtdataModel <- aov(Bd_load~Temperature,data=newtdata)
z <- summary(newtdatamodel)
list(Fval=unlist(z)[7],probF=unlist(z)[9])## $Fval
## F value1
## 9007.434
##
## $probF
## Pr(>F)1
## 1.543597e-266After changing the sample sizes several times, reducing my sample sizes all the way down to 2 for each group still results in significant differences. As I decreased the sample size, my p-value increased until it became closer and closer to 0.05. This indicates that this study did not need such a large sample size to find a significant difference, however large sample sizes can often increase the robustness of statistical tests, as it does in this instance.
Question 8 See text above.